Dipol - Puzzle - Hilfe

In dem linken Feld sind Dipole und nicht magnetische Blöcke angeordnet. Die Zahlen am Rand geben an, wieviel Pluspole und Minuspole in der jeweiligen Reihe oder Spalte vorhanden sind. Natürlich sollten gleich geladene Pole nicht zusammenstoßen.
Finde alle Dipole mit ihrer korrekten Anordnung sowie die nicht-magnetischen Blöcke.

Wenn du meinst, für ein Feld herausbekommen zu haben, ob und wie ein Block darin liegt, klicke erst einen Pol/Block an, dann das Feld, was diesen Pol beherbergen soll. Der Block wird automatisch zum Dipol oder Block ergänzt.

Es bedeuten:

Du kannst ein Puzzle zwischenspeichern, Cookies müssen dazu zugelassen sein.

Lösungsbeispiel Puzzle Teaser (6x6):

1. Schritt:
   

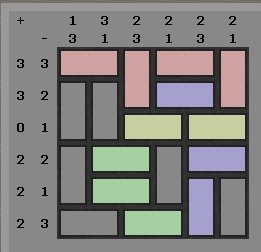
   Die oberste Reihe ist voll mit Magneten besetzt: die Anzahl der Ladungen ist gleich der Zeilenbreite. (rosa)

   Zeile 3 enthält nur ein negatives Feld. Das bedeutet: alle waagerecht liegenden Elemente, die geladen wären, würden ja 2 Ladungen mitbringen, was die Summe der Ladungen für die Reihe über schreitet. Das heisst weiterhin, alle waagerechten Elemente in dieser Reihe sind neutral. (beige)

   Die vorletzte Spalte enthält 5 Ladungen, das einzige neutrale Feld ist bereits festgelegt. Somit müssen alle Blöcke in der Spalte eine Ladung tragen. Welche, ist erst mal unbekannt.(rosa,blau)

   Gleiches gilt für die 3. Spalte.(rosa,grün)

   
   
2. Schritt:
   

   Die letzte Zeile enthält 5 Ladungen, eine neutrale Ecke. Für die neutrale Ecke kommt nur das Feld rechts unten in frage, das linke untere Feld würde zuviele Ladungen blockieren. (beige)

   Damit ist aber auch klar, dass das Feld links unten ein Dipol ist.(rosa)

   Reihe 2/Spalte 5: damit die Summe der Ladungen der Spalte erreicht werden kann, ist das Feld geladen.(grün)

   Reihe 4 und 5 weisen bereits genauso viele Ladungen auf wie am Rand angegeben, d.h. alle freien Blöcke sind ungeladen (blau).
   

3. Schritt:
   Nun betrachten wir die Einzelladungen der Spalte rechts aussen. Der oberste Stein verbrät eine positive und eine negative Ladung, da bleibt für den waagerechten weiter unten nur der Plus-Pol (rosa).

   Davon ausgehend können wir jetzt ein paar Ladungen eintragen.(grün)
   

4. Schritt:
   

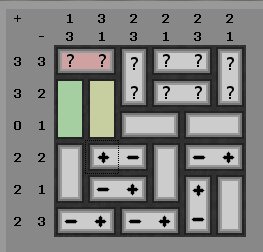
   In Spalte 2 fehlt noch eine positive Ladung, diese kann nur bei Zeile 1 sein (rosa). Damit ist die Ladungssumme für diese Spalte komplett, und der Stein darunter ist neutral (beige)

   Für den letzten Magneten bleibt nur noch der Platz in der 2.Reihe/1. Spalte, und weil die 3.Zeile nur eine negative Ladung enthält, muss der negative Pol dorthin. (grün)

   Jetzt noch vom letzten Magneten aus alle Ladungen eintragen...
   
5. Schritt:
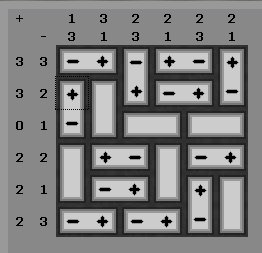   ... fertig ist die Laube!